Experimental Design and the Football Draw
Have you ever wondered about how the AFL football draw, or indeed any competitive sporting draw, is selected? Clearly (if you can remain unbiased!) it is desirable to give every team an equal opportunity to finish on top of the ladder, based on merit rather than luck. Ideally each team would play every other team the same number of times and under the same conditions. However, this is not always possible in practice. Constraints such as the number of available playing days, limiting each team to not more than one game each weekend, and balancing the number of home and away or evening and afternoon games all need to be taken into account.

What is the best way to achieve this balance?
Anyone who has experienced organising or participating in a tournament at a sports club will be aware of how hard it can be to ensure fairness for all teams. The writer personally experienced in her childhood an annual tennis tournament consisting of several doubles matches where in one year she won the tournament, and in the next year she received the "wooden spoon"!
These sporting draws are examples of experimental designs, where the aim is to find the best team or player, or to rate them on their playing ability. Usually, we can directly compare only two teams at any one time, but by carefully balancing which pairs of teams play and in which order, we are able to indirectly assess all teams relative to each other in an optimal way.
There are other specific constraints that need to be taken into account when selecting the AFL football draw. For example, the tradition that Collingwood and Essendon always play each other on Anzac Day and that the two Western Australian teams never have home games on the same weekend (except when playing each other, of course).
There are many parallels here with the design of experiments in the more traditional areas of industry and research, including agriculture, the environment, medical and other scientific settings.
Even for seemingly simple designs, the task can be complex. Sometimes decisions worth thousands or millions of dollars can rest on conclusions drawn from an experiment, so getting it right is crucial. Considerable mathematical and statistical theory has been developed over the years to cope with such problems - an internet search for "tournament design", for example, gives an indication of the breadth of this issue. There are different techniques to ensure fairness, and many different classes of experiment have been developed.
Figure 1, shows an historical forestry experiment laid out in a Latin Square design, which aims to simultaneously balance the effects of upper or lower slope and position across the slope.
Data Analysis Australia employs skilled mathematicians and statisticians with the training and experience to consider the many inter-related aspects necessary to design efficient and robust experiments.
What is an experiment?
An experiment is a study in which the experimenter controls or manipulates certain conditions, called experimental treatments, and measures outcomes or responses, so that it can be inferred that the treatment caused the outcome. This is different from an observational study in which associations can be demonstrated but causality cannot unambiguously be inferred. For example, it might be discovered that people are more likely to die if in a hospital than in their own home, but we should not conclude that hospitals are inherently unsafe - people who are more seriously ill tend to be taken to hospitals. (In fact, if the difference in illness levels was controlled for, we'd hope to find a smaller chance of dying in hospital than at home. However this is not a situation where we'd want to perform a formal experiment, randomly choosing whether to send a person to hospital or leave them at home!)
Why do we need specialist experimental design?
Resources for experiments are often limited or expensive, and it is desired to compare experimental treatments objectively, with minimum bias (the correct answer would be obtained, on average, if the experiment could be repeated many times) and minimum variability or uncertainty (how similar our answers would be if the experiment could be repeated many times). We say an experiment is efficient if it estimates the outcome variables with small variance, or high precision.
Maybe it doesn't matter so much for the football draw (though many might disagree vehemently!), but in an industrial setting where a single run might cost hundreds or thousands of dollars and multi-million-dollar decisions rest on conclusions drawn from the experiment, it becomes crucial to ensure biases and inefficiencies are eliminated or minimised in the experiment.
Engaging an experienced statistician from the early planning stages of an experiment can help ensure the following:
- The problem is formulated in a way suitable to experimentation and analysis;
- The experiment is planned and run to ensure it answers the questions of interest, with adequate and definable accuracy;
- Required resources are minimised while maintaining the desired accuracy - it is often too late to consider this once the data has been collected; and
- That the experimental design is optimised from a statistical point of view, which may enable you to answer more questions with no additional outlay.
A statistician can also apply general principles to cater for special considerations that might need to be taken into account, such as the requirement for particular football teams to play on Anzac Day, with minimal compromising of the desirable features of the experimental design.
The principal aims of experimental design are to minimise bias and increase precision, together resulting in improved accuracy.
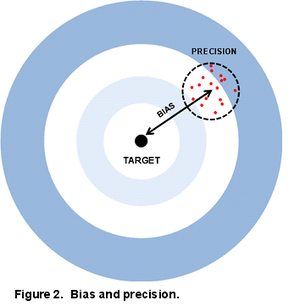
These concepts are often presented in terms of shots at a target. No bias means that hits are clustered around the centre of the target, while biased shots cluster off-centre. Precision means they are tightly placed around their centre, whether that is on-target or off-target. Accuracy is a combination of bias and precision. It is possible to have high precision but large bias and this gives us precise but inaccurate results, as in Figure 2.
High precision corresponds to small variance. Variability is everywhere in the world and estimated quantities are always subject to variation from many sources. Quantification of the uncertainty in estimates is one of the benefits of statistical analysis. Further, the uncertainty can be reduced by various techniques available to statisticians. However, bias is often less obvious and much harder to detect. Good experimental design strives to minimise bias as well as reduce variance.
There are many types of experimental designs and issues to be considered, including:
- Simple experiments where different experimental treatments are applied to equal numbers of experimental subjects or units, allocated randomly;
- Complex experiments with several different types of experimental treatments examined simultaneously (for example ratio of cake ingredients, quantity of mixture, size of cake tin, baking temperature, and baking time);
- Different sized experimental units (for example make or model of car and fuel composition - several different fuel compositions can be tested in the same car, but it is more expensive to obtain additional cars to test differences between cars; or in an agricultural experiment, it might be possible to plant different varieties of a plant in small plots, but fertiliser or watering regimes may only be possible to apply to larger areas - in this case we can get more sensitive results about varieties of plants than we can about fertiliser or watering regimes);
- Comparing different treatments on groups of similar individuals or under similar circumstances (such as the same weather conditions), in blocks - this reduces unwanted variation that is due to differences between individuals and allows a more sensitive comparison of the treatment effects:
- Typically, a block will contain just enough individuals for each experimental treatment to appear once under the same conditions, with multiple blocks to provide replication;
- Sometimes it is not possible to compare all the "treatments" in one block, such as in the football draw, where we can directly compare only two teams at a time - the blocks are smaller than the total number of treatments (teams) and are called incomplete blocks in the language of experimental design;
- There can be different levels of blocking, such as the two teams playing on a particular ground at a particular time, and all the teams playing on a particular weekend
A statistician can also help to determine which treatments to consider, and how to choose the subjects or experimental units. Modifying the number or type of treatments or treatment combinations and ensuring adequate controls
Replication
Replication is a critical aspect of experimental design. If each treatment appeared only once in the whole experiment, we would not know whether differences between the results were due to differences between the individuals themselves or truly due to the different treatments they received. Replication means applying each treatment to multiple individuals, and allows us to assess apparent treatment differences against the background natural variation.
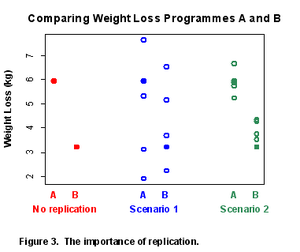
For example, suppose we wish to test two weight loss programmes, A and B. A person on Programme A achieves a 6.0 kg weight loss, while a person on Programme B achieves a 3.2 kg weight loss. Which Programme is better?
Without replication, we cannot tell whether typical results from the two programmes might actually be more like Scenario 1 or more like Scenario 2 shown in Figure 3. The conclusions would be very different.
Many differences between individuals will influence weight loss and add to variability.
In this example, since initial weight (or amount overweight) is likely to affect ease of weight loss, blocking would be an excellent idea - group together the most overweight people and assign an equal number to each programme, and similarly for less overweight groups.
Controls
In general it is wise to include controls or comparison individuals in an experiment. Controls are individuals that receive a standard treatment, or no treatment, or some other treatment for comparison - this would be called the control treatment. In the weight loss example, it might be good to also monitor the weight of a group of individuals who are not given a particular programme to follow but are selected from a similar group of people and treated similarly in every way other than the treatment. This gives added confidence to conclusions about the true effect of the treatments.
If the weight loss programme consisted of a drug in tablet form, some people could be given a dummy tablet that looks like the active drug but in fact is inactive, while otherwise being treated similarly. This form of control treatment is known as a placebo. You may have heard of the placebo effect. Even though the tablet should have no effect, people receiving a placebo often have a different response to those receiving no treatment at all. Including a placebo as an additional treatment is another way for the experimenter to be more confident that results came from the active ingredient in the drug.
An experiment can include more than one form of control, for example a placebo (inactive treatment), and no treatment.
Random allocation
Once the pool of experimental units or subjects and the set of treatments have been defined, the treatments should be allocated at random.
Randomness is a well-defined and objective way of selecting items or assigning treatments and is quite different to haphazard or arbitrary allocation, even though it might not appear so. Humans are particularly poor at selecting truly random numbers - they might tend to be too regular or avoid extremes. True random allocation requires an objective randomisation device such as dice, well mixed numbered balls, or a random number generator. Randomness helps reduce subjective bias (for example giving the new treatment to those subjects or experimental units that are more likely to respond well, in order to get a favourable result). Randomisation is a form of insurance against unwanted variation that you cannot "design out" by other means, such as blocking.
An example where the lack of objective random allocation can bias results is when a new cancer drug with much promise is being tested and, with the best of intentions, the person allocating patients to the treatments wants those who are most ill to be more likely to obtain the active drug rather than an inactive control. This could invalidate the results, or reduce the size of the effect observed, possibly even resulting in an experiment that appears to suggest the drug is not beneficial, thus denying or delaying benefit to others.
Ethics
This leads us into the topic of ethics, another important role of the statistician in designing experiments, especially those that involve human or animal subjects. The number of experimental subjects should not be larger than necessary to answer the question(s) of interest, but, perhaps even more importantly, the experiment should not be so small that it is likely to be inconclusive - in this case the whole experiment is wasted and another experiment is required.
Blinding
In addition to randomisation, another technique to reduce bias is called blinding. This means one or more of the participants in an experiment is unaware of ("blind to") which treatment they are receiving, so as to avoid bias, for example in the application of a treatment or in assessment of its effects.
Blinding typically occurs in medical experiments where one or more of those administering the treatment, the person receiving the treatment, and the person assessing the result might be unaware of the treatment - who is receiving a new drug, who is receiving a standard drug, and who is receiving an inactive control or placebo, for example. In any kind of taste test, blinding is highly desirable, whether or not a physical blindfold is used.
Not all experimental treatments are amenable to blinding. For example different forms of treatment that cannot be made to appear indistinguishable, such as treatment with and without surgery, or with and without counselling - although in some cases an assessor of the outcome could be blinded to (unaware of) the treatment the subject had received.
Easier analysis
Another benefit of consulting a statistician at the planning stage is that it can make the statistical analysis of the results simpler and more robust. More straightforward analysis can mean not only that the analysis is quicker and cheaper to perform, but also that it is easier to interpret and explain and more transparent to an audience. Assumptions are made in all statistical analyses, for example about the distribution of data and independence of different observations. Good experimental design will help ensure these assumptions are close to the truth, so that there can be greater confidence in the conclusions.
Your input
To help design efficient experiments that answer the required questions, the statistician will need some background information from you. Decisions will be made jointly between you and the statistician. Sometimes a pilot study is valuable to enable better planning of the full study and/or to test or refine experimental techniques and protocols. Some issues to consider are:
- The types of responses you expect to measure and how they might vary amongst the subjects or units in the experiment;
- The size or importance of differences between different treatments that you expect;
- How sure you want to be that you will detect that size of difference if it is present;
- How many subjects or units are feasible for you to use;
- Restrictions on the application of the treatments;
- How many can be tested at once;
- How long it takes;
- Any other factors that might contribute to differences in the response being measured; and
- Whether these factors can or cannot be controlled to help reduce unwanted variability or "noise" and therefore give a more efficient experiment.
Thinking about such issues before you talk with the statistician will be valuable preparation.
Further information
For a high quality experiment with sound, reliable conclusions and realistic indications of precision in your results, consult with an experienced statistician in the early stages of your experiment.
This article is a brief outline of only a few aspects of experimental design and is not intended to be a textbook introduction - there are many other considerations to which a statistician can contribute and add value. If you wish to discuss any of the issues raised in this article in relation to your own work, or other aspects of experimental design or analysis, please contact Data Analysis Australia, and a consultant statistician will be pleased to talk with you.
December 2011
