Making Sense of Complex Data
Data often comes in droughts and floods - sometimes there is not enough to make good decisions and at other times there is too much data to comprehend. Today, the problem is often the complexity created by the large number of variables observed.
This is seen in many situations. In mining, modern analytical equipment can analyse many elements at once. In social research, a survey can collect dozens of separate items of information for each person interviewed. In genomics, it is possible to measure thousands of genes and hundreds of thousands of nucleotides for each individual. Imaging data from a camera or by remote sensing measures light in several colours at millions of pixels.
Statisticians describe such challenging data as high dimensional. There are simply too many variables, each one possibly relating to the rest, to think about at once. Even the first step of exploring data visually is difficult. If there were just two variables they could be plotted on paper or a computer screen, so that the eye can do what it does best - find patterns. Three dimensions can be imagined since we live in a 3-D world and many computer packages now enable three dimensional graphs to be drawn. But most people, including statisticians, have difficulty thinking and visualising in four dimensions and beyond. So what do you do when you get 10 or 20 variables of interest - or even hundreds or thousands?
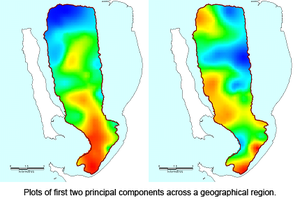
A solution is to reduce the dimensions without losing too much information within the data. Karl Pearson, a statistician (as well as a scholar of medieval German literature, a lawyer and social activist), developed an approach called Principal Component Analysis (PCA) in 1901. This used mathematics to optimally combine many variables together to give only a single variable (or few variables - called principal components) which can then be considered by the user. A measure of Pearson's insight is that to this day, it remains the most frequently used method of reducing the number of dimensions of a complex dataset.
Since then a variety of related methods have been developed - factor analysis and multidimensional scaling to give just two - which simplify and present complex data. Some of these methods not only reduce the dimensions but also make the dimensions meaningful.
So how can these principal components be used and what can they tell us? First, they enable us to plot them, by considering only the first two or three components, which encapsulate the information from all the variables. Secondly, they often have meaning. A very pervasive example today is seen in personality tests such as the commonly used Myers-Briggs Type Indicator®. These tests typically use up to 100 questions but reduce the results down to just a few dimensions and give names such as introversion-extraversion to these dimensions.
Alternatively, some methods can largely sidestep the problem of high dimensions. Cluster analysis and other segmentation methods can be applied often with little concern about individual variables, rapidly reducing the data to a few groups of similar observations. Looking at typical values for each group, the variables can often be readily understood. In marketing, this amounts to giving "typical individuals" for each group, providing a good way of designing tailored marketing approaches.
Making sense of complex data using tools such as PCA and cluster analysis are everyday occurrences at Data Analysis Australia. They may be the main analysis, or a useful tool in understanding the data for further analysis. They can even be used together. The key to their success is in being able to understand and use their statistical underpinnings in conjunction with considered thought and interpretation - it is often said that statistics is more of an art than a science, and techniques such as these epitomise the blending of the two.
For further information on how Data Analysis Australia can help using these methods, please Contact Us.
March 2012
